Polinomlarda işlemler konusunda sınavlarda daha çok bölme işlemiyle ilgili sorular karşımıza çıkmaktadır. Yani “Polinomlarda bölme” başlığının polinomlar konusunun bel kemiği olduğunu söyleyebiliriz. Bu yüzden bölme dışındaki polinom işlemlerine daha yüzeysel yaklaşmak doğru olacaktır.
Polinomlarda toplama ve çıkarma derecesi aynı olan terimler üzerinden yapılır.
Derecesi aynı olan terimlerin katsayıları işleme konur.
Polinomlarda Toplama
Polinomlarda toplama tıpkı denklemlerde yapılan toplama gibi aynen yapılır.
Örnek:
P(x)= 3x7+5x2+3, Q(x)= 2x8+4x2 olsun.
Derecesi aynı olan terimlerin katsayıları toplanır, diğerleri ise oluşan toplam polinomuna aynen eklenir.
Yani P(x)+Q(x)=N(x) ise T(x)= 3x7+5x2+3+2x8+4x2=2x8+3x7+9x2+3‘dir.
Polinomlarda Çıkarma
Polinomlarda toplama tıpkı denklemlerde yapılan toplama gibi aynen yapılır.
Örnek:
P(x)= 3x8+5x2+3, Q(x)= 2x8+4x2 olsun.
Derecesi aynı olan terimlerin katsayıları çıkarılır, diğerleri ise oluşan fark polinomuna aynen yazılır.
Yani P(x)-Q(x)=N(x) ise F(x)= 3x8+5x2+3–(2x8+4x2)=x8+x2+3‘tür.
Polinomlarda çarpma ve bölme, üslerin toplanması ve çıkarılması ile yapılır.
Üslü ifadelerde işlemler gibi çarparken üsler toplanır, bölerken üsler çıkarılır.
Polinomlarda Çarpma
Polinomlarda çarpma yapılırken üsler toplanır.
Örnek:
P(x)= x2+5x2+3, Q(x)=x+2x2 olsun.
Çarpılan terimlerin üsleri toplanır.
Yani P(x).Q(x)=N(x) ise N(x)= (x2+5x2+3) (x+2x2) = x2.x + x2.2x2 + 5x2.x + 5x2.2x2 + 3.x + 3.2x2 =x3+2x4+5x3+10x4+3x+6x2
=12x4+6x3+6x2+3x
Polinomlarda Bölme
Polinomlarda bölme çok başlıklı bir konudur. Bölme sırasında işlemler uzun sürdüğünden dolayı doğrudan yapmak yerine kısayollar kullanılarak yapılır. Bu yüzden daha ayrıntılı incelenmesi gereken bir konudur.
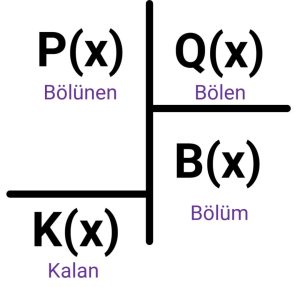
Normal bir bölme tablosunda olduğu gibi P(x)=Q(x).B(x)+k(x) ve der[k(x)] < der[Q(x)]
Örnek bir polinomlarda bölme işlemi:
P(x)= x2+2x+3 polinomun x-2’ye bölelim.



Polinomlarda bölme işleminde kalan bulma
Yukarıdaki polinomlarda bölme işleminde gördüğümüz üzere bölme tablosunu çizerek 11 kalanına ulaşabiliriz. Fakat sınavlarda öğrencilerden istenen bu değildir. Kalanı kısaca bulmak için bölen ifadeyi “0” yapan x değerini kullanacağız.
Örnek:
P(x)= 5x2+3 olsun. P(x)’in x-2‘ye bölümünden kalanı bulmak için x-2‘yi “0”a eşitleriz ve x=2 olur.
Bu durumda kalan, P(2)=23 olacaktır.
Polinomlarda tam bölünme
Sorularda eğer bir polinomun bir terime tam bölündüğü ifade ediliyorsa polinomun ilgili terim için değeri “0”dır.
Önerilen Yazılar:
